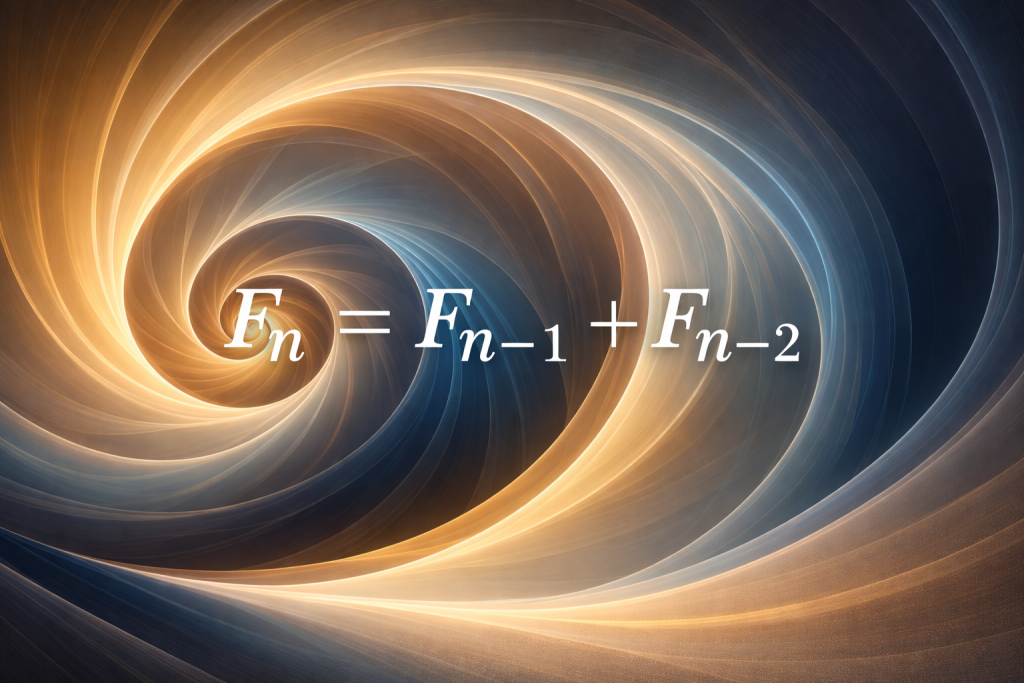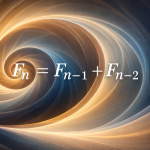À l’école, il y a deux catégories de mathématiques.
Celles qui traumatisent à vie… et celles qui, avec un peu de recul, deviennent franchement réjouissantes.
La suite de Fibonacci fait partie de la seconde catégorie, même si on ne s’en rend compte que bien plus tard.
Le principe est pourtant enfantin : chaque nombre est la somme des deux précédents.
0, 1, 1, 2, 3, 5, 8, 13…
Rien de magique. Pas de sortilège. Juste une idée simple : on avance avec ce qu’on a déjà.
Dit autrement : rien ne sort de nulle part.
Ni les mathématiques. Ni les économies. Ni les sociétés.
Et c’est là que Fibonacci devient intéressant.
Détail souvent oublié : Leonardo Fibonacci n’a pas seulement appris les mathématiques dans les livres européens. Né à Pise, dans une république maritime ouverte sur le monde, il a été formé en grande partie à Béjaïa, au Maghreb central, l’actuelle Algérie. Son père, Guglielmo Bonacci, y travaillait comme marchand et notaire des douanes pour le compte de la république de Pise. Autrement dit, cette suite que l’on croit abstraite est aussi le produit d’un monde de flux, d’échanges commerciaux, de circulations de savoirs entre rives de la Méditerranée.
Une économie, comme une suite de Fibonacci, vit de mémoire.
Ce qu’elle produit aujourd’hui dépend de ce qu’elle a produit hier… et avant-hier.
Des compétences, des institutions, des règles, des habitudes, des réflexes. Tout cela circule, se transmet, se transforme — ou pas.
Quand les choses vont bien, les flux circulent : l’argent, les idées, les initiatives, les talents.
Quand les choses vont moins bien, les flux tournent en rond. Ils circulent toujours, mais dans un périmètre de plus en plus étroit. Comme un manège qui n’emmène plus nulle part.
L’économie algérienne, vue sous cet angle, est un excellent cas d’école.
Depuis des décennies, elle fonctionne sur une équation assez stable :
la rente des hydrocarbures, additionnée à des institutions héritées d’un autre temps.
Cette combinaison a longtemps fait le travail. Elle a amorti les chocs, financé la redistribution, évité des crises majeures. On aurait tort de le nier.
Mais, comme dans une suite de Fibonacci à laquelle on n’ajoute jamais d’information réellement nouvelle, arrive un moment où la dynamique devient parfaitement prévisible… puis s’essouffle.
Ça ne s’arrête pas brutalement.
Ça ralentit.
Puis ça stagne.
On continue à additionner hier et avant-hier, mais sans enrichir l’équation par une information nouvelle. Résultat : l’économie tourne… mais sur une boucle courte.
C’est un peu comme annoncer régulièrement un nouveau départ, tout en s’assurant soigneusement de ne surtout pas quitter le même quai. Les annonces se succèdent, les chiffres défilent, l’impression de mouvement est là… Mais le train, lui, reste à l’arrêt.
On entend souvent que le problème vient de la non-convertibilité, des lourdeurs administratives, des réglementations. C’est partiellement vrai. Mais ce sont des symptômes, pas la maladie.
Le vrai sujet est plus simple, et plus politique : quand le système se crispe, il préfère contrôler les flux plutôt que les organiser. L’initiative devient suspecte. L’erreur devient dangereuse. L’expérimentation devient un luxe.
Alors on protège ce qui existe. On fige ce qui fonctionne encore. Et, sans le vouloir vraiment, on empêche ce qui pourrait fonctionner autrement. Dans ces conditions, les flux ne disparaissent pas. Ils continuent de circuler. Mais ils ne s’élargissent plus.
Or une économie vivante n’est pas celle qui évite tout changement.
C’est celle qui accepte d’ajouter de nouveaux termes à l’équation.
De nouvelles idées.
De nouveaux acteurs.
De nouvelles façons de faire.
Allonger la boucle, ce n’est pas renier le passé.
C’est lui donner une suite.
Et c’est là que Fibonacci devient presque optimiste.
Car cette suite nous dit autre chose, plus réjouissante : tant qu’on ajoute quelque chose — même modeste — la dynamique repart. Ce n’est pas la taille du saut qui compte. C’est le fait d’en faire un.
En mathématiques comme en économie, le vrai danger n’est pas l’erreur.
C’est la reproduction confortable du même schéma.
Voilà pourquoi Fibonacci mérite mieux que quelques lignes oubliées dans un manuel scolaire.
Il nous rappelle, avec une élégance désarmante, qu’un système ne meurt pas parce qu’il avance trop vite…
mais parce qu’il n’avance plus que sur lui-même.
____________________________________________________________________________________________
Cet article n’a pas vocation à clore un sujet.
Au contraire. Il ouvre un cycle de contributions qui tenteront de faire le lien entre les mathématiques et notre quotidien, sans intimidation intellectuelle ni révérence excessive. Fibonacci en est l’épisode 1, presque naturellement : simple en apparence, riche dès qu’on s’y attarde.
L’idée n’est pas de transformer les mathématiques en prétexte philosophique, mais de rappeler qu’elles sont souvent plus proches de nos vies qu’on ne l’imagine. Elles décrivent des rythmes, des équilibres, des répétitions, des ruptures. Bref, des choses très humaines.
Ce cycle se veut aussi participatif. Les lecteurs qui le souhaitent sont invités à proposer des pistes, des intuitions, des exemples. L’exercice est sans doute plus spontané lorsqu’il s’agit de physique — la chute des corps, le temps, l’espace parlent facilement à l’imaginaire. Les mathématiques, elles, demandent un léger pas de côté. Mais une fois ce pas franchi, elles deviennent un véritable régal pour l’esprit.
Rendez-vous donc pour l’épisode 2.